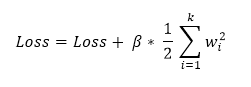L2 and Dropout Regularization in Neural Network Classification

Overfitting has been one of the most common problems you will face while performing any machine learning technique. To overcome this we have two regularization techniques L2 and Dropout. We will see the accuracy comparison with and without the regularization.

I believe that you have practiced well with the Neural Network using TensorFlow. If not take a look at the Classification using NN.

The Regularization is used to penalize the large values of weights that prevent the model to converge. Before proceeding towards the python code, I would like to clear the two concepts the L2 and Dropout. These two techniques can be used together.

L2 Regularization

The L2 regularization adds a term in the loss function which is given by:

It sums the squares of all the respective weights, then divide it by 2 and then multiply with a small constant which needs to be tuned. From the code below it would make you further clear.

For L2, replace the loss with the following:

loss= tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits,tf_train_labels) + 0.01 *       tf.nn.l2_loss(weights['h1']) + 0.01 *tf.nn.l2_loss(weights['out']))

Dropout

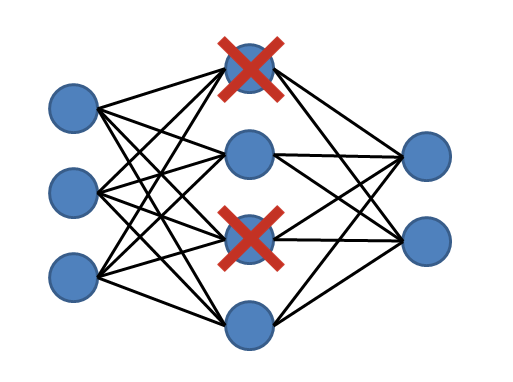
Itis a technique in which the hidden layer output is dropped with respect to thekeep probability. In our case the hidden layer output is fed into the outputlayer with a probability of 0.5. For example if there are two outputs from the ReLu, then 0.5 probability would keep one of them randomly. So during training, this would keep different outputs every time in every iteration thus doing justice with all the weighted values and helping the converge to converge.

Below is the basic structure of Neural Network explaining the Dropout with 0.5 prob.

Dropout must only be used for the training dataset.
Fromthe code perspective there will be a slight change in it. Add the below function after the Neural Network function:

def Neural_Network_dropout (x, weights, biases):
    keep_prob = tf.Variable(0.5,tf.float32)
    # Hidden layer with RELU activation
    layer_1 = tf.add(tf.matmul(x, weights['h1']), biases['b1'])
    hidden_layer = tf.nn.relu(layer_1)
    drop = tf.nn.dropout(hidden_layer,keep_prob)
     # Output layer with linear activation
    out_layer = tf.matmul(drop, weights['out']) + biases['out']
    return out_layer

Also replace the logits assignment with:

logits= Neural_Network_dropout(tf_train_dataset, weights, biases)

In case of full code, check out my Tensorflow GitHub Repo.

Now its time for you to play with the code, make some changes, used each technique separately and compare the accuracy, compare with the previous version of it.

I got a slight increase in the accuracy with L2, same for the dropout, but when I used both the accuracy decreased in my case. The decrease is mainly because of the number of steps, we used only 801 steps, and it would work well if you increase it to atleast 14001 steps. Remember this would take time, may be around 30 to 50min.

I will recommend you to try the multi-layer neural network, it is very easy. Hint: You just have to change both the Neural Network functions. In case of help you can get the full code from the repo.

In the next article I would share how parameters tuning would impact the accuracy.